К содержанию
Составитель к.ф.-м.н. Подклетнова С.В.
Лекция 1. Уравнения высших порядков. Задача Коши. Некоторые частные случаи
дифференциальных уравнений высшего порядка
1.1. Определение дифференциальных уравнений
высших порядков
Зачастую при решении технических, физических и
экономических вопросов учёные натыкаются на проблему поиска функции из
некоторого уравнения, содержащего не только саму функцию и аргументы, от которых
она зависит, но и её производные. Такие уравнения, как нам уже известно,
называются дифференциальными уравнениями.
Существуют дифференциальные уравнения, зависящие от одного
или нескольких аргументов. В случае если в дифференциальном уравнении существует
лишь один аргумент, его называют обыкновенным дифференциальным уравнением. Если
у дифференциального уравнения несколько аргументов, то говорят о
дифференциальном уравнении в частных производных.
Если в уравнение входит производная
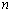 -го
порядка искомой функции
-го
порядка искомой функции 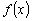 ,
но не входят производные более высоких порядков, то такое уравнение называется
уравнением
,
но не входят производные более высоких порядков, то такое уравнение называется
уравнением 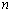 -го
порядка.
-го
порядка.
Ранее вы ознакомились с обыкновенными дифференциальными
уравнениями первого порядка. В настоящем курсе будем рассматривать
дифференциальные уравнения высших порядков, то есть те обыкновенные
дифференциальные уравнения, порядок которых не меньше двух.
Дадим следующее определение:
Определение 1.1. Уравнение вида
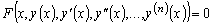 (1.1)
(1.1)
при
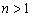 называется
уравнением
называется
уравнением 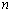 -го
порядка относительно функции
-го
порядка относительно функции 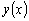 .
.
Если мы сможем выразить из уравнения (1.1) производную
высшего порядка, то есть привести уравнение (1.1) к виду:
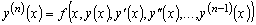 ,
(1.2)
,
(1.2)
то говорят, что полученное
уравнение называется дифференциальным уравнением
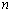 -го
порядка в нормальной форме.
-го
порядка в нормальной форме.
1.2. Общее и частное решение дифференциального уравнения.
Задача Коши
В предыдущем курсе уже говорилось о том, что
дифференциальные уравнения первого порядка могут иметь частные и общее решение.
Это же правило распространяется и на дифференциальные уравнения высших порядков.
Напомним, что существование целой системы решений дифференциальных уравнений,
отличающихся лишь на константу, вызвано тем, что производная функции
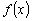 и
производная функции
и
производная функции 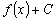 являются
одной и той же величиной. Поэтому при расчёте общего интеграла дифференциального
уравнения как слагаемое появляется некоторая постоянная величина. И такое
решение, охватывающее все возможные комбинации решений дифференциального
уравнения, называется общим решением. В случае же, если нам известно
значение константы
являются
одной и той же величиной. Поэтому при расчёте общего интеграла дифференциального
уравнения как слагаемое появляется некоторая постоянная величина. И такое
решение, охватывающее все возможные комбинации решений дифференциального
уравнения, называется общим решением. В случае же, если нам известно
значение константы 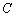 ,
мы будем говорить о частном решении данного дифференциального уравнения.
,
мы будем говорить о частном решении данного дифференциального уравнения.
Очевидно, если мы имеем дифференциальное уравнение
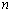 -го
порядка, для получения решения которого нужно взять
-го
порядка, для получения решения которого нужно взять
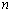 интегралов,
то и его общее решение должно содержать
интегралов,
то и его общее решение должно содержать
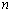 констант.
констант.
Зачастую в постановке задачи известны значения самой
функции и её производных в какой-то точке
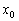 .
В этом случае говорят, что заданы начальные условия задачи.
.
В этом случае говорят, что заданы начальные условия задачи.
Начальными условиями (ещё их называют условиями Коши) для
дифференциального уравнения 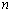 -го
порядка (1.1) называются значение функции и её первых
-го
порядка (1.1) называются значение функции и её первых
 производных
в некоторой точке
производных
в некоторой точке 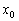 .
.
Задачей Коши называется задача отыскания частного
решения уравнения (1.1):
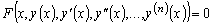 ,
,
Удовлетворяющего начальным условиям
(условиям Коши):
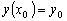 ,
,
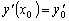 ,
,
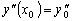 ,
(1.3)
,
(1.3)
…
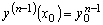 .
.
Очевидно, что при решении такой задачи, мы получим частное
решение дифференциального уравнения (1.1).
Ранее мы дали понятие общего решения дифференциального
уравнения, теперь дадим точное определение этого понятия.
Определение 1.2. Общим решением
дифференциального уравнения 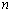 -го
порядка в некоторой области
-го
порядка в некоторой области 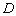 ,
в каждой точке которой и в её окрестности функция
,
в каждой точке которой и в её окрестности функция
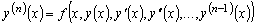 непрерывна
и имеет в этой окрестности частные производные
непрерывна
и имеет в этой окрестности частные производные
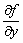 ,
,
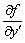 ,
,
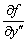 ,…,
,…,
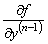 ,
называется
,
называется 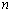 -параметрическое
семейство функций
-параметрическое
семейство функций 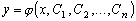 ,
удовлетворяющее следующим условиям:
,
удовлетворяющее следующим условиям:
1)
непрерывно дифференцируемая функция
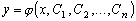 является
решением уравнения (1.2) при любых значениях произвольных постоянных
является
решением уравнения (1.2) при любых значениях произвольных постоянных
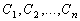 ;
;
2)
при любых начальных условиях (1.3) существуют такие значения постоянных
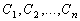 ,
что функция
,
что функция 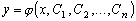 удовлетворяет
этим условиям.
удовлетворяет
этим условиям.
Решение дифференциального уравнения (1.1), полученное в
неявном виде:
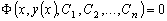 ,
,
называется общим интегралом
этого уравнения.
Геометрически общее решение (или общий интеграл)
дифференциального уравнения (1.1) изображается в виде семейства интегральных
кривых на плоскости, зависящих от 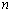 параметров.
параметров.
Пусть дано дифференциальное уравнение
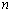 -го
порядка в нормальной форме (1.2) и система начальных условий (1.3).
-го
порядка в нормальной форме (1.2) и система начальных условий (1.3).
Сформулируем без доказательства следующую теорему:
Теорема 1.1 (о существовании и единственности
решения задачи Коши). Если функция
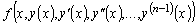
непрерывна в окрестности некоторой
точки
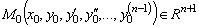
и имеет в этой окрестности
непрерывные частные производные 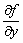 ,
,
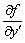 ,
,
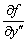 ,…,
,…,
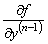 ,
то найдётся интервал
,
то найдётся интервал  ,
на котором существует и притом единственное решение задачи Коши
,
на котором существует и притом единственное решение задачи Коши
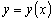 .
.
1.3. Решение некоторых видов дифференциальных уравнений высшего порядка
Очевидно, что в случае, если мы сможем свести
дифференциальное уравнение высшего порядка к уравнению первого порядка, то
решить полученное уравнение не составит труда теми методами, которые были
рассмотрены в предыдущем курсе математического анализа. Сведение уравнение более
высокого порядка к уравнению порядком ниже называется понижением порядка. Сейчас
мы рассмотрим некоторые случаи, в которых данное дифференциальное уравнений
высшего порядка может быть упрощено понижением его порядка.
Самое простое из таких уравнений – уравнение вида:
 (1.4)
(1.4)
Решается данное дифференциальное уравнение последовательным
понижением его порядка.
Обозначим 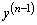 через
через
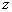 .
Тогда
.
Тогда
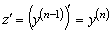 .
.
И уравнение (1.4) принимает вид
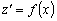 .
.
Простым интегрированием находим:
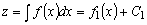 .
.
Порядок исходного уравнения понизился на единицу. Получили:
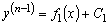 .
.
Теперь обозначим
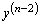 через
через
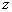 .
Тогда
.
Тогда
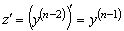 .
.
И
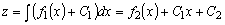 .
.
То есть
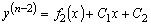 .
.
Далее последовательно интегрируя уравнение подобным
образом, приходим к его общему решению.
Для нахождения частного решения задачи Коши нужно
подставить в полученное общее решение начальные условия Коши и выявить
последовательно все неизвестные константы
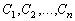 .
.
Пример 1.1. Найти общее решение уравнения
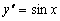 и
частное решение, удовлетворяющее краевым условиям:
и
частное решение, удовлетворяющее краевым условиям:
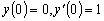 .
.
Решение.
Сначала найдём общее решение заданного уравнение его
последовательным интегрированием:
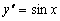 ,
,
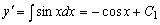 ,
,
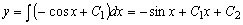 ,
,
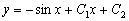 –
искомое общее решение.
–
искомое общее решение.
Подставим условия задачи Коши:
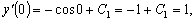
отсюда
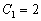
и
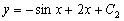 .
.
 ,
,
тогда
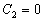 ,
,
а
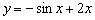 –
частное решение задачи Коши для данного уравнения с поставленными начальными
условиями.
–
частное решение задачи Коши для данного уравнения с поставленными начальными
условиями.
Другой вид уравнений, допускающих понижение порядка:
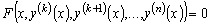 .
(1.5)
.
(1.5)
Уравнение (1.5) не содержит в явном виде искомой функции и
производных до  порядка
включительно. Его можно привести к уравнению порядка
порядка
включительно. Его можно привести к уравнению порядка
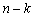 с
помощью замены
с
помощью замены 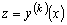 .
.
Тогда
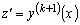 ,
,
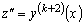 ,
,
…
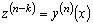 .
.
Поэтому уравнение (1.5) приводится к виду:
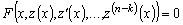 .
.
Порядок последнего уравнения
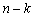 .
.
Далее интегрируем полученное уравнение, находим новую
искомую функцию 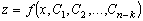 ,
которая обратной заменой сведётся к виду:
,
которая обратной заменой сведётся к виду:
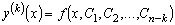 ,
,
который рассмотрен нами раньше.
Пример 1.2. Найти общее решение уравнения
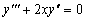 .
.
Решение.
Пусть
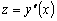 .
.
Тогда
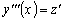 .
.
И данное уравнение принимает вид:
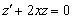 .
.
Это уравнение с разделяющимися переменными. Разделим
переменные:
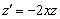 ,
,
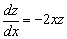 ,
,
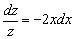 ,
,
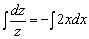 ,
,
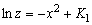 ,
,
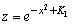 ,
,
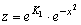 ,
,
 ,
,
где
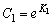 .
.
Производим обратную замену:
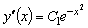 .
.
Дважды интегрируем:
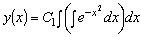 –
общее решение данного дифференциального уравнения.
–
общее решение данного дифференциального уравнения.
Последний вид уравнений, допускающий понижение порядка,
который мы рассмотрим в настоящем курсе, – уравнение, не содержащее в явном виде
аргумент 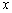 :
:
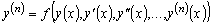 .
(1.6)
.
(1.6)
Для решения этого уравнения применяется следующий
искусственный приём: примем 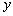 новым
аргументом уравнения, а за искомую функцию возьмём
новым
аргументом уравнения, а за искомую функцию возьмём
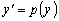 .
.
Поскольку
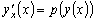 ,
,
то
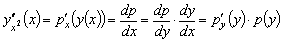
и так далее.
Для примера рассмотрим случай уравнения второго порядка, то
есть уравнение вида:
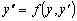 .
(1.7)
.
(1.7)
Произведя вышепоказанную замену, получим:
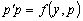 ,
,
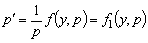 .
.
А это уравнение решается простым интегрированием.
Затем делается обратная замена и производится повторное
интегрирование.
Для примера рассмотрим следующую задачу.
Пример 1.3. Материальная точка
 (маятник)
массой
(маятник)
массой 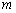 подвешена
на нерастяжимой нити длиной
подвешена
на нерастяжимой нити длиной 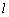 ,
массой которой можно пренебречь. Маятник выведен из положения равновесия, а
затем отпущен. Точка
,
массой которой можно пренебречь. Маятник выведен из положения равновесия, а
затем отпущен. Точка 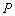 начинает
двигаться по окружности радиуса
начинает
двигаться по окружности радиуса 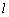 ,
расположенной в вертикальной плоскости (рис. 1.1). Найти закон движения
маятника, если он в начальный момент времени
,
расположенной в вертикальной плоскости (рис. 1.1). Найти закон движения
маятника, если он в начальный момент времени
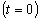 отклонен
от положения равновесия на угол
отклонен
от положения равновесия на угол 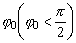 и
имеет начальную скорость, равную нулю.
и
имеет начальную скорость, равную нулю.
Решение.
![]() и
заменим
и
заменим ![]() на
на
![]() :
:![]() (1.8)
(1.8)![]() ,
то есть относится к виду уравнений, не содержащих явно независимой переменной.
,
то есть относится к виду уравнений, не содержащих явно независимой переменной.![]() ,
,![]() .
.![]() –
уравнение с разделяющимися переменными.
–
уравнение с разделяющимися переменными.![]() .
.![]() .
.![]() является
угловой скоростью, то при
является
угловой скоростью, то при ![]() выполняется:
выполняется:![]() и
и
![]() .
.![]() получим:
получим:![]() ,
,![]() ,
,![]()
![]() .
.![]() угол
угол
![]() убывает,
то производная
убывает,
то производная ![]() отрицательна,
следовательно,
отрицательна,
следовательно,![]() .
.![]() ,
то
,
то![]() –
уравнение с разделяющимися переменными.
–
уравнение с разделяющимися переменными.![]() .
.![]() .
(1.9)
.
(1.9)![]() .
.![]()