Занятие № 4. Дивергенция векторного поля.
Теорема Гаусса-Остроградского

1. Дивергенция векторного поля

Задание 4.1.1. Дать определение и физический смысл дивергенции векторного поля.

Задание 4.1.2. Сформулировать и доказать теорему о дивергенции векторного поля.

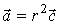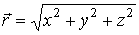Пример 4.1.1. Найти дивергенцию поля , где  и 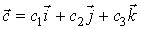 – постоянный вектор.

Решение.

I способ (по теореме о дивергенции).

,

.

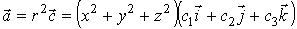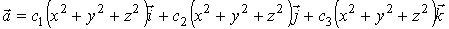Следовательно,

,

,

.

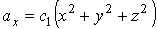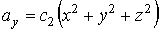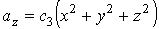Тогда по теореме о дивергенции

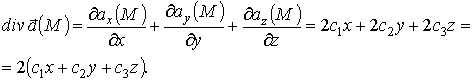
II способ (по свойствам дивергенции).

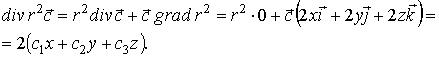
Упражнения.

1.             Найти дивергенцию поля 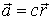, где 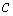 – постоянный скаляр.

2.             Найти дивергенцию поля 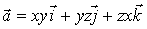 в точке .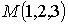

3.             Найти дивергенцию поля 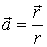, где .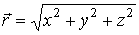

4.             Найти дивергенцию поля 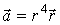, где .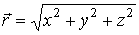

5.             Найти дивергенцию поля линейных скоростей 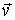 частиц жидкости, вращающейся вокруг оси 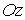 с постоянной угловой скоростью : .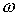

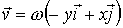6.             Найти дивергенцию поля .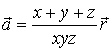

2. Теорема Гаусса-Остроградского.

Задание 4.2.1. Сформулировать и доказать теорему о дивергенции векторного поля.

Пример 4.2.1. Найти поток вектора 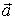 через замкнутую поверхность 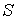, ограничивающую объем 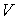, если дивергенция вектора 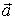 во всех точках поля есть постоянная величина .

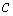Решение.

По теореме Гаусса-Остроградского имеем:

.

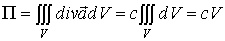Пример 4.2.2. Вычислить поток поля вектора 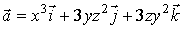 через поверхность сферы .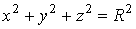

Решение.

Найдем дивергенцию вектора :

.

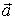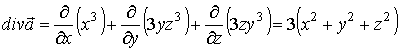Согласно теореме Гаусса-Остроградского

.

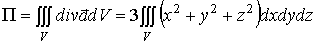Перейдем к сферическим координатам:

; .

.

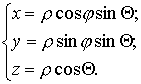
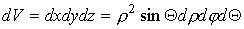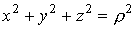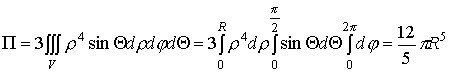Упражнения.

7.             Найти поток вектора 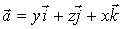 через полную поверхность пирамиды, ограниченную плоскостями , , ,  .

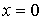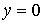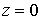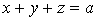
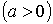8.             Найти поток вектора 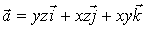 через полную поверхность пирамиды с вершинами в точках , , , .

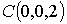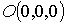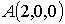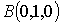9.             Найти поток поля вектора 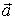 через поверхность сферы , .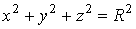

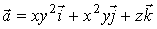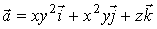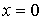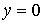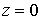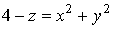10.        Найти поток поля вектора  через замкнутую поверхность, образованную плоскостями: , ,  и частью поверхности параболоида , лежащую в первом октанте.