Занятие № 6. Теорема Стокса.

Задание 6.1. Сформулировать и доказать теорему Стокса.

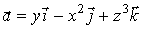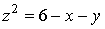Пример 6.1. Вычислить циркуляцию поля вектора  по линии пересечения поверхности  с координатными плоскостями в положительном направлении.

Решение.

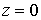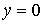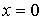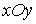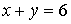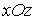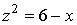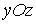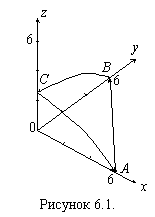
Полагая последовательно , , , находим линии пересечения поверхности с координатными плоскостями соответственно:  – по прямой ;  – по параболе ;  – по параболе 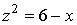 (рисунок 6.1). На чертеже указано направление положительного обхода контура 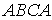. Вычислим циркуляцию поля при помощи теоремы Стокса.

Согласно теореме Стокса:

Циркуляция поля 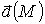 по контуру L равна потоку вихря поля через любую поверхность S, лежащую в векторном поле и имеющую своей границей контур L:

При этом предполагается, что на поверхности S все частные
производные первого порядка от функций а_х, а_у, а_z непрерывны.

Вычислим вихрь вектора :

.

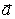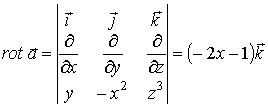В качестве поверхности 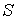 возьмем боковую поверхность пирамиды 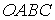: 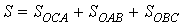. Применяя теорему Стокса, получим:

.

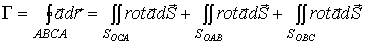На грани 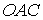 вектор 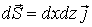, поэтому

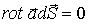 и .

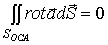На грани 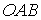 вектор 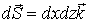, поэтому

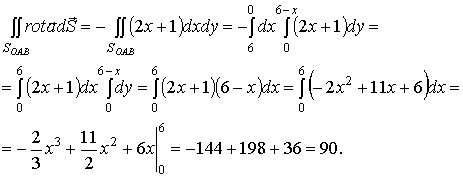
На грани 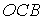 вектор 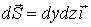, поэтому

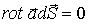 и .

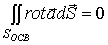Окончательно получим

.

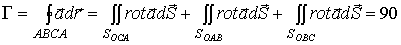Упражнения.

1.             Используя теорему Стокса, найти циркуляцию поля вектора 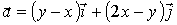 по контуру 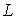, состоящему из координатных осей и дуги окружности 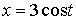, , 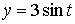соответствующей параметру .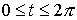

2.             Найти линейный интеграл вектора 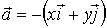 по дуге эллипса 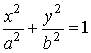, лежащей в первом квадранте, используя теорему Стокса.

3.             Найти циркуляцию векторного поля 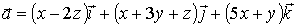 по контуру треугольника , где , , .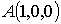

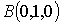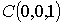4.             Найти циркуляцию векторного поля 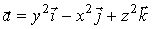 по контуру пересечения координатных плоскостей с поверхностью .
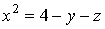