Занятие № 7. Соленоидальное и
потенциальное поля
1. Соленоидальное поле
Задание 7.1.1. Дать определение
соленоидального поля.
Задание 7.1.2. Физический смысл
соленоидального поля.
Пример 7.1.1. Покажем, что поле напряженности
магнитного поля, образованного электрическим током, текущим по бесконечному
прямолинейному проводу, соленоидально всюду, за исключением начала координат.
Решение.
Вектор напряженности магнитного поля
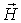 определяется
формулой
определяется
формулой
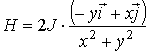 .
.
Вычислим дивергенцию
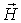 по
формуле
по
формуле
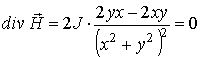 .
.
Отсюда видно, что поле
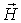 всюду
соленоидально, за исключением начала координат, где оно вообще не определено.
Векторными линиями поля
всюду
соленоидально, за исключением начала координат, где оно вообще не определено.
Векторными линиями поля 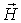 ,
как известно из физики, являются концентрические окружности, центр которых на
проводе, то есть замкнутые линии.
,
как известно из физики, являются концентрические окружности, центр которых на
проводе, то есть замкнутые линии.
Упражнения.
1.
Будут ли векторные поля следующих векторов соленоидальными?
а) 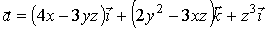 ;
;
б) 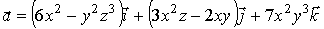 .
.
2. Потенциальное поле
Задание 7.2.1. Дать определение
потенциального поля.
Задание 7.2.2. Сформулировать и доказать
признак потенциальности поля.
Задание 7.2.3. Сформулировать и доказать
свойства потенциального поля.
Пример 7.2.1. Будет ли поле вектора
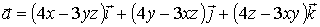 потенциально?
В случае потенциальности поля найти потенциальную функцию
потенциально?
В случае потенциальности поля найти потенциальную функцию
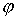 .
.
Решение.
Найдем вихрь данного поля:
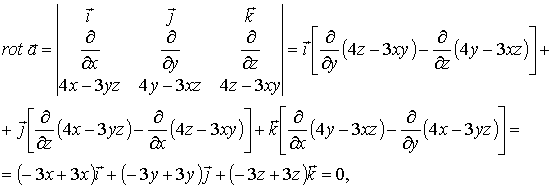
следовательно, поле потенциально.
Найдем теперь его потенциальную функцию
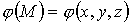 :
:
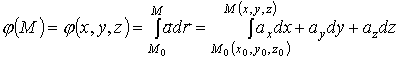 .
.
В качестве начальной точки
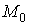 выберем
начало координат. Согласно третьему свойству потенциального поля
криволинейный интеграл в потенциальном поле не зависит от пути интегрирования.
Для практического вычисления функции
выберем
начало координат. Согласно третьему свойству потенциального поля
криволинейный интеграл в потенциальном поле не зависит от пути интегрирования.
Для практического вычисления функции
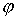 удобнее
всего брать в качестве пути
удобнее
всего брать в качестве пути 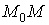 ломаную
ломаную
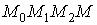 ,
изображенную на рисунке 7.1.
,
изображенную на рисунке 7.1.
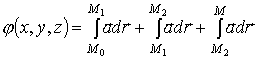
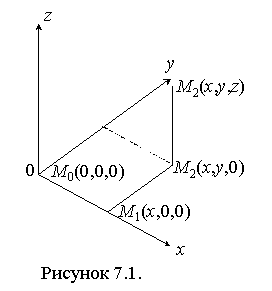 .
.
Вычислим отдельно каждый из этих интегралов.
1) 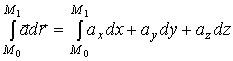 .
.
На отрезке 
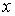 меняется
от 0 до значения
меняется
от 0 до значения 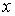 точки
точки
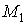 ,
,
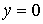 ,
,
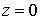 ,
значит
,
значит 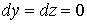 и
и
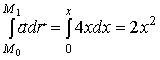 .
.
2) На отрезке 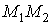 меняется
только
меняется
только 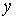 от
0 до
от
0 до 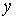 ,
,
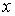 постоянен,
постоянен,
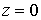 ,
поэтому
,
поэтому 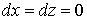 и
и
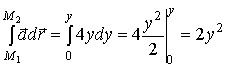 .
.
3) На отрезке 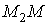 меняется
только
меняется
только 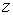 от
0 до
от
0 до 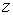 ,
,
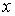 и
и
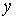 постоянны,
поэтому
постоянны,
поэтому 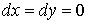 и
и
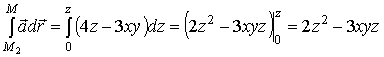 .
.
Следовательно, потенциальная функция
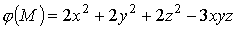 .
.
Упражнения.
2. Будут
ли поле вектора 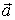 потенциально?
В случае потенциальности поля найти потенциальную функцию
потенциально?
В случае потенциальности поля найти потенциальную функцию
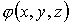 .
.
а) 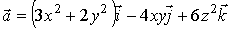 ;
;
б) 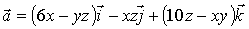 .
.