Занятие № 9. Решение задач, повторение
1. Дана функция
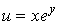 и
точки
и
точки 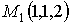 и
и
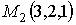 .
Вычислить: 1) Производную функции
.
Вычислить: 1) Производную функции 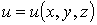 в
точке
в
точке 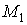 по
направлению вектора
по
направлению вектора 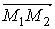 ;
2)
;
2) 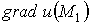 .
.
Решение.
1)
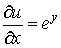 ;
;
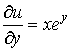 ;
;
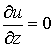 ;
;
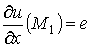 ;
;
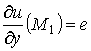 ;
;
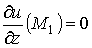 ;
;
единичный вектор 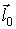 направления
направления
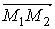 :
:
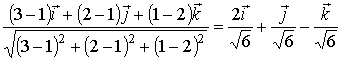 ,
,
отсюда получаем:
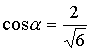 ;
;
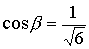 ;
;
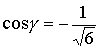 .
.

2)
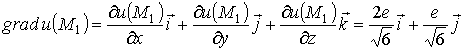 .
.
2. Даны
векторное поле 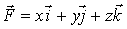 и
плоскость
и
плоскость 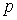 :
:
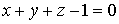 ,
которая совместно с координатными плоскостями образует пирамиду
,
которая совместно с координатными плоскостями образует пирамиду
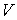 .
Пусть
.
Пусть  –
основание пирамиды, принадлежащее плоскости
–
основание пирамиды, принадлежащее плоскости
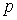 ;
;
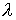 –
контур, ограничивающий
–
контур, ограничивающий  ,
,
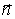 –
нормаль к
–
нормаль к  ,
направленная вне пирамиды
,
направленная вне пирамиды 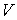 .
Требуется вычислить: 1) поток векторного поля
.
Требуется вычислить: 1) поток векторного поля
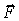 через
поверхность
через
поверхность  в
направлении нормали
в
направлении нормали 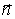 ;
2) циркуляцию векторного поля
;
2) циркуляцию векторного поля 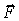 по
замкнутому контуру
по
замкнутому контуру 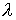 непосредственно
и применив теорему Стокса к контуру
непосредственно
и применив теорему Стокса к контуру 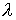 и
ограниченной им поверхностью
и
ограниченной им поверхностью  с
нормалью
с
нормалью 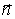 ;
3) поток векторного поля
;
3) поток векторного поля 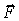 через
полную поверхность пирамиды
через
полную поверхность пирамиды 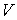 в
направлении внеш
в
направлении внеш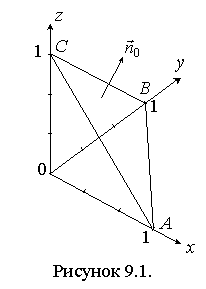 ней
нормали к ее поверхности непосредственно и применив теорему
Гаусса-Остроградского. Сделать чертеж.
ней
нормали к ее поверхности непосредственно и применив теорему
Гаусса-Остроградского. Сделать чертеж.
Решение.
1)
Найдем линию пересечения данной плоскости с координатной плоскостью
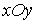 .
Для этого положим
.
Для этого положим 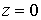 .
Тогда
.
Тогда
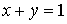 .
.
Линия пересечения данной плоскости с координатной
плоскостью 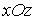 (
(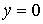 )
задается уравнением
)
задается уравнением
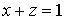 ,
,
а линия пересечения данной
плоскости с координатной плоскостью 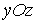 (
(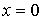 )
– уравнением
)
– уравнением
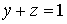 .
.
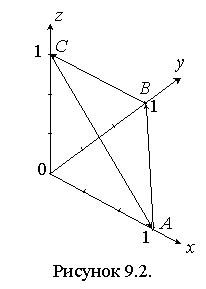
Вычислим поток поля через площадь треугольника
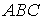 (рисунок
3.2).
(рисунок
3.2).
За положительное направление нормали
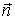 к
плоскости треугольника примем направление от начала координат:
к
плоскости треугольника примем направление от начала координат:
 .
.
Тогда
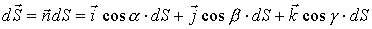 .
.
Так как в нашем случае все направляюще косинусы
положительны, имеем
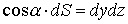 ;
;
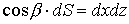 ;
;
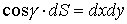 .
.
Поэтому
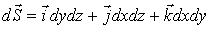 ,
,
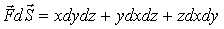 .
.
Искомый поток поля будет состоять из трех поверхностных
интегралов по площади треугольника 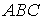 :
:
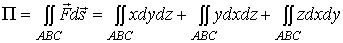 .
.
Каждый из этих трех поверхностных интегралов заменим
двойным интегралом, являющимся проекцией треугольника на соответствующую
координатную плоскость.
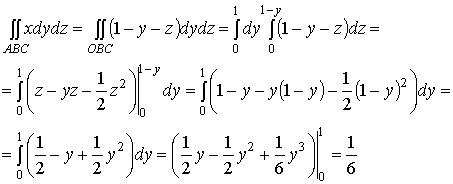
 Аналогично
заменяются и два других поверхностных интеграла двойными:
Аналогично
заменяются и два других поверхностных интеграла двойными:
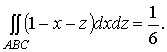
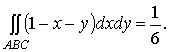
Отсюда 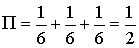 .
.
2)
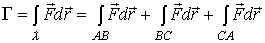
На
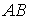
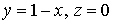 ,
,
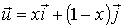 ,
,
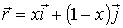 ,
,
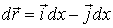 ,
,
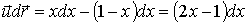 .
.
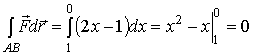 .
.
Аналогично,
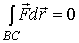 ,
,
 .
.
Тогда
 .
.
По теореме Стокса
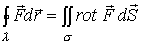
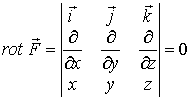
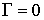 .
.
3)
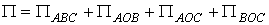
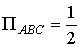 (см.
1)).
(см.
1)).
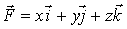
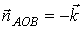 .
.

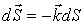
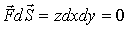 ,
т.к. на
,
т.к. на 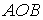
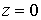 ,
,
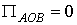 .
.
Аналогично,
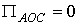 ,
,
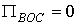 .
.
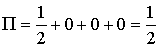 .
.
По теореме
Остроградского-Гаусса
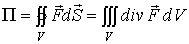 .
.
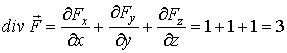 .
.
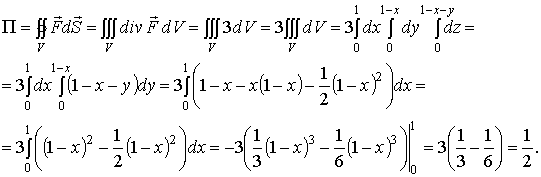
3. Проверить,
является ли векторное поле 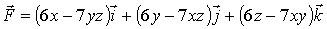 потенциальным
и соленоидальным. В случае потенциальности поля
потенциальным
и соленоидальным. В случае потенциальности поля
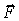 найти
его потенциал.
найти
его потенциал.
Решение.
Найдем вихрь данного поля:
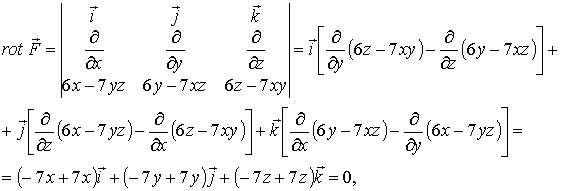
следовательно, поле потенциально.
Найдем теперь его потенциальную функцию
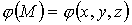 :
:
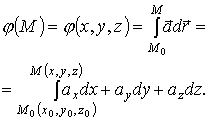
В качестве начальной точки
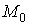 выберем
начало координат. Согласно третьему свойству потенциального поля
криволинейный интеграл в потенциальном поле не зависит от пути интегрирования.
Для практического вычисления функции
выберем
начало координат. Согласно третьему свойству потенциального поля
криволинейный интеграл в потенциальном поле не зависит от пути интегрирования.
Для практического вычисления функции
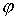 удобнее
всего брать в качестве пути
удобнее
всего брать в качестве пути 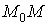 ломаную
ломаную
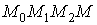 ,
изображенную на рисунке 7.1.
,
изображенную на рисунке 7.1.
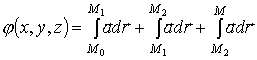 .
.
Вычислим отдельно каждый из этих интегралов.
1) 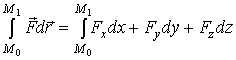 .
.
На отрезке 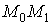
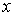 меняется
от 0 до значения
меняется
от 0 до значения 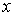 точки
точки
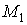 ,
,
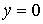 ,
,
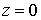 ,
значит
,
значит 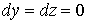 и
и
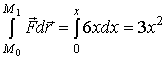 .
.
2) На отрезке 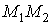 меняется
только
меняется
только 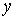 от
0 до
от
0 до 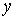 ,
,
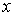 постоянен,
постоянен,
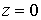 ,
поэтому
,
поэтому 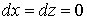 и
и
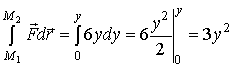 .
.
3) На отрезке 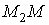 меняется
только
меняется
только  от
0 до
от
0 до  ,
,
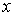 и
и
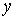 постоянны,
поэтому
постоянны,
поэтому 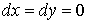 и
и
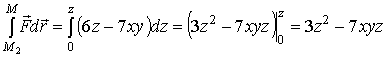 .
.
Следовательно, потенциальная функция
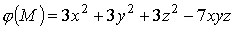 ,
,
а потенциал:
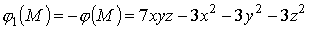 .
.
Проверим, является ли поле
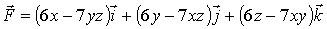 соленоидальным.
соленоидальным.
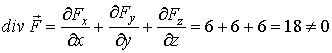 ,
,
следовательно, данное поле не
соленоидально.
1. Вычислить поток вектора
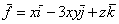 через
поверхность
через
поверхность 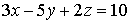 ,
,
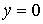 ,
,
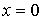 ,
,
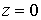 .
.
Решение.
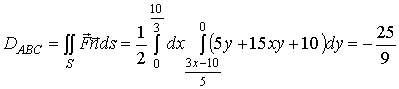 ,
,
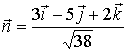 ,
,
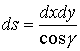 ,
,
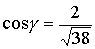 .
.
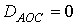 ,
,
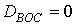 ,
,
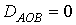 ,
,
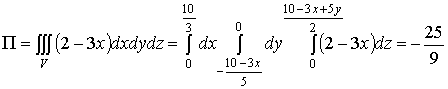 .
.