К содержанию
Составитель к.ф.-м.н. Подклетнова С.В.
Лекция 3. Линейные дифференциальные операторы. Общее решение линейного
дифференциального уравнения
3.1. Линейные дифференциальные операторы и их свойства
Определение 3.1. Оператором называется
отображение 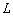 ,
ставящее в соответствие каждой функции
,
ставящее в соответствие каждой функции
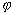 из
некоторого множества другую функцию
из
некоторого множества другую функцию 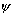 :
:
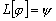 .
.
Пример 3.1. Оператор умножения на функцию
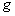 ставит
в соответствие каждой функции
ставит
в соответствие каждой функции 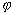 функцию
функцию
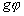 .
Например
.
Например 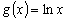 ,
,
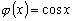 ,
то значение
,
то значение  в
точке
в
точке 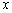 равно
равно
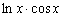 .
.
Пример 3.2. Оператор дифференцирования
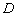 на
промежутке
на
промежутке 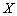 ставит
в соответствие каждой функции
ставит
в соответствие каждой функции 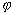 ,
дифференцируемой на этом промежутке, её производную (рассматриваемую на этом же
промежутке):
,
дифференцируемой на этом промежутке, её производную (рассматриваемую на этом же
промежутке):
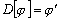 .
.
Определение 3.2.
Суммой операторов 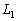 и
и
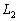 называется
оператор
называется
оператор 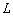 такой,
что
такой,
что 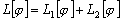 .
Будем его обозначать
.
Будем его обозначать
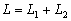 .
.
Определение 3.3. Произведением операторов
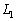 и
и
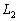 называют
оператор
называют
оператор 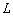 такой,
что
такой,
что 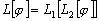 .
Его обозначают
.
Его обозначают 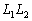 .
.
Пример 3.3. Оператор
 ставит
в соответствие функции
ставит
в соответствие функции 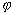 функцию
функцию
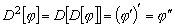 .
Вообще
.
Вообще 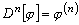 .
.
Определение 3.4. Оператор
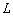 называют
линейным, если для любых функций
называют
линейным, если для любых функций 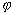 и
и
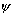 ,
к которым он применим, и любого числа
,
к которым он применим, и любого числа
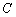 выполняются
равенства:
выполняются
равенства:
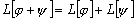
и
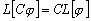 .
.
Пример 3.4. Оператор умножения на функцию
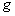 линеен,
так как если
линеен,
так как если 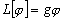 ,
то
,
то
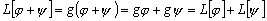 ,
,
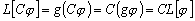 .
.
Пример 3.5. Оператор дифференцирования
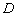 линеен,
так как по правилам дифференцирования
линеен,
так как по правилам дифференцирования
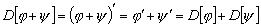 ,
,
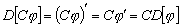 .
.
Сумма и произведение линейных отображений (в частности,
линейных операторов) линейны. Таким образом, если операторы
 и
и
 линейные,
то и операторы
линейные,
то и операторы  и
и
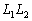 линейны.
линейны.
Из линейности операторов дифференцирования и умножения,
показанной в примерах 3.4 и 3.5 следует линейность любого оператора вида
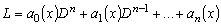 .
(3.1)
.
(3.1)
Определение 3.5. Оператор (3.1) называется
линейным дифференциальным оператором
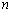 -го
порядка.
-го
порядка.
Лемма 3.1. Если
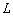 –
линейный оператор,
–
линейный оператор, 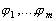 –
некоторые функции и
–
некоторые функции и 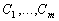 –
некоторые постоянные, то
–
некоторые постоянные, то
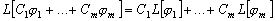 .
(3.2)
.
(3.2)
Доказательство.
Доказательство проведём методом математической индукции.
При 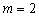
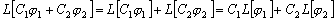 .
.
Предположим, что равенство (3.2) справедливо при
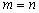 ,
то есть выполняется
,
то есть выполняется
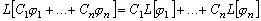 .
.
Пусть 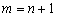 ,
тогда
,
тогда
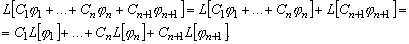
В предположении, что равенство (3.2) справедливо при
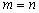 мы
доказали, что оно справедливо при
мы
доказали, что оно справедливо при 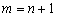 .
.
Лемма доказана.
3.2. Общее решение однородного
линейного дифференциального уравнения
Пусть задан линейный дифференциальный оператор
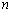 -го
порядка (3.1). Тогда уравнение вида
-го
порядка (3.1). Тогда уравнение вида
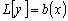 (3.3)
(3.3)
изображает линейное
дифференциальное уравнение 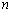 -го
порядка:
-го
порядка:
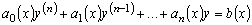 .
(3.4)
.
(3.4)
Теорема 3.1. Пусть функции
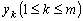 являются
соответственно решениями уравнений
являются
соответственно решениями уравнений
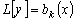
с одинаковой левой частью, а
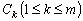 суть
константы. Тогда функция
суть
константы. Тогда функция

является решением уравнения
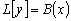 ,
,
где
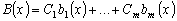 .
.
Доказательство.
По условию для любого
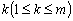 выполняется
равенство
выполняется
равенство 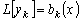 .
Согласно лемме 3.1
.
Согласно лемме 3.1

Следовательно, функция
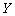 удовлетворяет
уравнению
удовлетворяет
уравнению 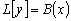 ,
что и требовалось доказать.
,
что и требовалось доказать.
Если в теореме 3.1 все
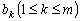 тождественно
равны нулю (то есть и функция
тождественно
равны нулю (то есть и функция 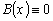 при
любых значениях
при
любых значениях 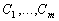 )
уравнение (3.3) становится однородным:
)
уравнение (3.3) становится однородным:
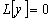 .
(3.5)
.
(3.5)
Следовательно, справедливо следствие.
Следствие 3.1. Если функции
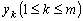 являются
решениями однородного линейного дифференциального уравнения
являются
решениями однородного линейного дифференциального уравнения
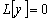 ,
,
а
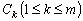 суть
константы. Тогда любая линейная комбинация
суть
константы. Тогда любая линейная комбинация
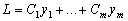
этих функций является решением
этого же уравнения.
Таким образом, совокупность решений линейного уравнения
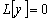 образует
линейное пространство.
образует
линейное пространство.
Примем без доказательства следующую теорему.
Теорема 3.2. Пусть на промежутке
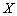 непрерывны
коэффициенты приведённого однородного линейного дифференциального уравнения
непрерывны
коэффициенты приведённого однородного линейного дифференциального уравнения
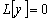 порядка
порядка
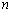 :
:
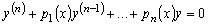 ,
(3.6)
,
(3.6)
тогда размерность пространства
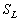 решений
этого уравнения на промежутке
решений
этого уравнения на промежутке 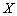 равна
равна
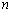 .
.
Эта теорема означает, что существует
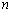 линейно
независимых решений уравнения
линейно
независимых решений уравнения 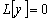 ,
причём любое решение
,
причём любое решение 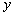 этого
уравнения на
этого
уравнения на 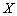 является
линейной комбинацией указанных решений:
является
линейной комбинацией указанных решений:
 .
(3.7)
.
(3.7)
Так как в выражение (3.7) входят
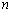 произвольных
постоянных
произвольных
постоянных 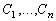 и
путём подбора этих постоянных можно получить любое решение
и
путём подбора этих постоянных можно получить любое решение
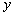 уравнения
(3.6) (а тем самым удовлетворить любым начальным условиям Коши), то (3.7)
является общим решением уравнения (3.6).
уравнения
(3.6) (а тем самым удовлетворить любым начальным условиям Коши), то (3.7)
является общим решением уравнения (3.6).
Теорема 3.3. Пусть на
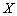 непрерывны
коэффициенты приведённого однородного линейного дифференциального уравнения
непрерывны
коэффициенты приведённого однородного линейного дифференциального уравнения
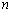 -го
порядка (3.6). Тогда общее решение этого уравнения на
-го
порядка (3.6). Тогда общее решение этого уравнения на
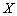 имеет
вид (3.7), где
имеет
вид (3.7), где 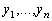 –
любая система, состоящая из
–
любая система, состоящая из 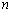 линейно
независимых решений данного уравнения.
линейно
независимых решений данного уравнения.
Определение 3.6. Систему функций, образующую
базис в пространстве 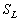 решений
линейного однородного уравнения
решений
линейного однородного уравнения 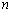 -го
порядка
-го
порядка 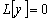 ,
называют фундаментальной системой решений этого уравнения.
,
называют фундаментальной системой решений этого уравнения.
Фундаментальная система решений состоит из
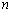 линейно
независимых решений этого уравнения.
линейно
независимых решений этого уравнения.
Определения 3.7. Определителем Вронского (или
вронскианом) называется определитель вида:
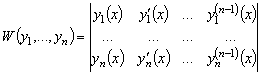 ,
,
где
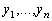 –
фундаментальная система решений уравнения (3.6).
–
фундаментальная система решений уравнения (3.6).
Теорема 3.4. Для линейной независимости
решений 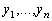 уравнения
(3.6) необходимо и достаточно, чтобы вронскиан
уравнения
(3.6) необходимо и достаточно, чтобы вронскиан
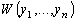 этих
решений был отличен от нуля в некоторой точке
этих
решений был отличен от нуля в некоторой точке
 промежутка
промежутка
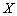 .
В этом случае он будет отличен от нуля и в остальных точках этого же промежутка.
.
В этом случае он будет отличен от нуля и в остальных точках этого же промежутка.
Пример 3.6. Доказать, что выражение
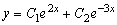 является
общим решением уравнения
является
общим решением уравнения
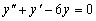 .
(3.8)
.
(3.8)
Доказательство.
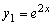 ,
,
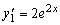 ,
,
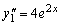 .
.
 ,
,
то есть
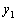 является
решением уравнения (3.8).
является
решением уравнения (3.8).
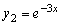 ,
,
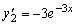 ,
,
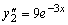 .
.
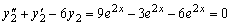 ,
,
то есть
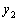 является
решением уравнения (3.8).
является
решением уравнения (3.8).
Вронскиан
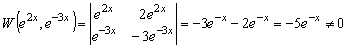 .
.
Значит, по теореме (3.4)
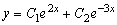 –
общее решение уравнения (3.8).
–
общее решение уравнения (3.8).
3.3. Общее решение неоднородного
линейного дифференциального уравнения
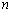 -го
порядка
-го
порядка
Пусть 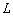 –
линейный дифференциальный оператор
–
линейный дифференциальный оператор 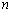 -го
порядка:
-го
порядка:
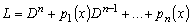 .
(3.9)
.
(3.9)
Тогда
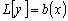 –
(3.10)
–
(3.10)
неоднородное линейное уравнение
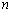 -го
порядка.
-го
порядка.
Уравнение
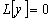 –
(3.11)
–
(3.11)
соответствующее уравнению (3.10)
однородное линейное уравнение 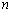 -го
порядка.
-го
порядка.
Теорема 3.5. Общее решение неоднородного
линейного дифференциального уравнения (3.10) равно сумме
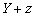 общего
решения
общего
решения 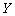 соответствующего
однородного уравнения (3.11) и какого-либо частного решения
соответствующего
однородного уравнения (3.11) и какого-либо частного решения
 уравнения
(3.10).
уравнения
(3.10).
Доказательство.
Так как 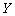 –
общее решение уравнения (3.11), то при любых значениях произвольных постоянных
имеем
–
общее решение уравнения (3.11), то при любых значениях произвольных постоянных
имеем 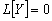 .
.
 –
решение уравнения (3.10) , поэтому
–
решение уравнения (3.10) , поэтому 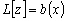 .
Из теоремы 3.3 получаем, что
.
Из теоремы 3.3 получаем, что 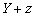 –
решение уравнения (3.10). Осталось показать, что
–
решение уравнения (3.10). Осталось показать, что
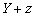 является
общим решением этого уравнения, то есть что путём подбора произвольных
постоянных это решение можно удовлетворить любым начальным условиям Коши:
является
общим решением этого уравнения, то есть что путём подбора произвольных
постоянных это решение можно удовлетворить любым начальным условиям Коши:
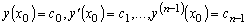 .
.
Так как
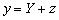 ,
,
то
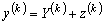 .
.
Тогда равенство
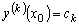
равносильно
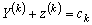 .
.
Тогда
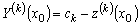 .
(3.12)
.
(3.12)
Поэтому достаточно подобрать произвольные постоянные
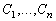 так,
чтобы выполнялись условия (3.12).
так,
чтобы выполнялись условия (3.12).
Так как 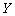 –
общее решение уравнения
–
общее решение уравнения 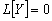 ,
то такой подбор произвольных постоянных возможен. Следовательно, функция
,
то такой подбор произвольных постоянных возможен. Следовательно, функция
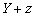 является
общим решением уравнения (3.10), что и требовалось доказать.
является
общим решением уравнения (3.10), что и требовалось доказать.
3.4. Метод вариации произвольных постоянных
Теорема 3.5 сводит отыскание общего решения неоднородного
линейного уравнения (3.10) к отысканию общего решения соответствующего
однородного уравнения (3.11) и любого частного решения неоднородного уравнения
(3.10).
На самом деле, зная общее решение соответствующего
однородного уравнения можно с помощью квадратур (вычисления интегралов) найти
частное решение неоднородного уравнения.
Рассмотрим сначала случай линейного дифференциального
уравнения второго порядка.
Будем искать частное решение уравнения (3.10) в виде
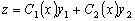 ,
(3.13)
,
(3.13)
где
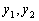 –
фундаментальная система решений,
–
фундаментальная система решений, 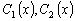 –
искомые функции.
–
искомые функции.
Из выражения (3.13) следует, что
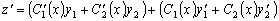 .
(3.14)
.
(3.14)
Общее число искомых функций равно двум, поэтому мы можем
сами наложить на них ещё одно условие:
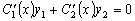 .
(3.15)
.
(3.15)
Тогда
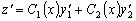 .
(3.16)
.
(3.16)
Отсюда
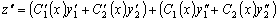 .
(3.17)
.
(3.17)
Подставим выражения (3.13), (3.16) и (3.17) в левую часть
уравнения 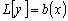 ,
где
,
где
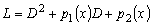 .
.
Так как
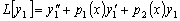 ,
,
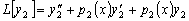 ,
,
то
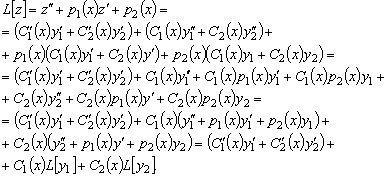
По условию 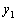 и
и
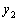 –
решения однородного уравнения
–
решения однородного уравнения 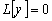 .
Значит,
.
Значит,
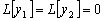
и
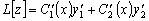 .
.
Поэтому уравнение
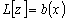 принимает
вид:
принимает
вид:
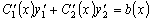 .
(3.18)
.
(3.18)
Таким образом, для отыскания неизвестных функций
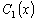 и
и
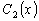 достаточно
решить систему двух уравнений (3.15) и (3.18):
достаточно
решить систему двух уравнений (3.15) и (3.18):
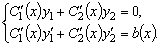 (3.19)
(3.19)
Определитель этой системы уравнений равен
 и
в силу линейной независимости функций
и
в силу линейной независимости функций
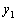 и
и
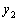 отличен
от нуля. Поэтому система уравнений (3.19) разрешима относительно функций
отличен
от нуля. Поэтому система уравнений (3.19) разрешима относительно функций
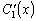 и
и
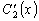 .
.
После решения системы (3.19) достаточно вычислить интегралы
от полученных значений функций 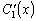 и
и
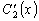 ,
а затем найти функцию
,
а затем найти функцию 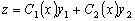 .
.
Для уравнения 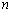 -го
порядка подобная система имеет вид:
-го
порядка подобная система имеет вид:
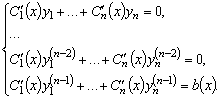 (3.20)
(3.20)
Пример 3.7. Найти методом вариации постоянных
общее решение уравнения
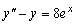 .
(3.21)
.
(3.21)
Решение.
Соответствующее однородное уравнение:
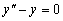 .
(3.22)
.
(3.22)
Легко убедиться, что функции
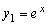 и
и
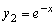 составляют
фундаментальную систему решений уравнения (3.22).
составляют
фундаментальную систему решений уравнения (3.22).
Его общим решением будет
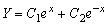 .
(3.23)
.
(3.23)
Будем искать частное решение уравнения (3.21) в виде:
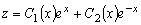 .
.
Для отыскания 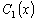 и
и
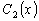 запишем
систему уравнений (3.19):
запишем
систему уравнений (3.19):
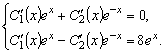
Сложим уравнения системы:
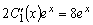 ,
,
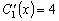 .
(3.24)
.
(3.24)
Теперь вычтем из второго уравнения первое:
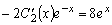
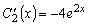 .
(3.25)
.
(3.25)
Интегрируем полученные выражения (3.24) и (3.25):
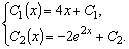
Отсюда частные решения (при
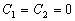 ):
):

Частное решение уравнения (3.21) запишется в виде:
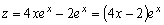 (3.26)
(3.26)
И общее решение данного уравнения (3.21), равное сумме
частного решение (3.25) и общего решения (3.23), будет следующим:
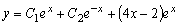 .
.
Ответ. 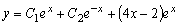
К содержанию