К содержанию
Составитель к.ф.-м.н. Подклетнова С.В.
Лекция 4. Линейные дифференциальные уравнения
высшего порядка с постоянными коэффициентами.
Численные методы Эйлера и Рунге-Кутта
4.1. Алгебра дифференциальных операторов.
Характеристический многочлен
Рассмотрим уравнение вида
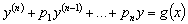 (4.1)
(4.1)
где
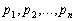 –
постоянные числа.
–
постоянные числа.
Определение 4.1. Уравнение (4.1) называют
линейным дифференциальным уравнением с постоянными коэффициентами.
Умножение дифференциальных операторов обладает свойством
ассоциативности, но в общем случае не является коммутативным. В то же время
сложение дифференциальных операторов дистрибутивно относительно сложения (как
слева, так и справа). Некоммутативность умножения дифференциальных операторов
влечет за собой различия между алгеброй таких операторов и обычной алгеброй. Но
есть класс дифференциальных операторов, для которых умножение коммутативно, а
именно класс линейных дифференциальных операторов с постоянными коэффициентами,
т.е. операторов вида
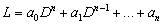 ,
,
где
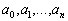 —
константы.
—
константы.
Назовём такие операторы дифференциальными многочленами.
Коэффициенты этих многочленов могут быть комплексными, но в этом курсе мы будем
иметь дело с дифференциальными многочленами, имеющими действительные
коэффициенты. Чтобы доказать коммутативность умножения дифференциальных
операторов с постоянными коэффициентами, достаточно заметить, что по свойствам
дифференцирования
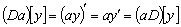
и
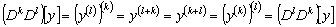 .
.
Поскольку операции сложения и умножения дифференциальных
многочленов обладают теми же свойствами, что и соответствующие операции над
числами, алгебра дифференциальных многочленов аналогична обычной алгебре
многочленов.
Определение 4.2. Многочлен
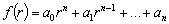 ,
,
в котором переменная
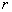 принимает
числовые значения, называют характеристическим многочленом для дифференциального
многочлена
принимает
числовые значения, называют характеристическим многочленом для дифференциального
многочлена
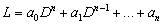 ,
,
а уравнение
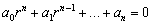 —
характеристическим уравнением для L.
—
характеристическим уравнением для L.
Каждому тождеству для обычных многочленов соответствует
тождество для дифференциальных многочленов.
Известная теорема:
Теорема 4.1. Любой многочлен f (r)
степени n можно представить в виде
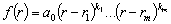 ,
,
где
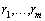 –
корни этого многочлена, a
–
корни этого многочлена, a 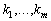 –
кратности этих корней. При этом
–
кратности этих корней. При этом 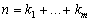 .
.
Даже в случае, когда коэффициенты многочлена действительны,
среди корней 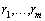 могут
быть и комплексные. Но тогда вместе с каждым комплексным корнем
могут
быть и комплексные. Но тогда вместе с каждым комплексным корнем
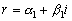 в
разложение входит сопряженный с ним корень
в
разложение входит сопряженный с ним корень
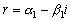 ,
и притом с той же кратностью.
,
и притом с той же кратностью.
Из теоремы 4.1 вытекает, что любой дифференциальный
многочлен
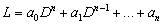
порядка n
можно разложить на множители:
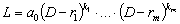 ,
,
где
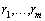 –
корни характеристического многочлена
–
корни характеристического многочлена
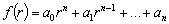 для
L, a
для
L, a 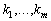 –
кратности этих корней. Это позволяет свести изучение любых дифференциальных
многочленов к изучению дифференциальных выражений вида
–
кратности этих корней. Это позволяет свести изучение любых дифференциальных
многочленов к изучению дифференциальных выражений вида
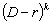 .
Докажем следующее утверждение:
.
Докажем следующее утверждение:
Теорема 4.2. Если
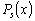 –
многочлен степени s и
–
многочлен степени s и 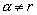 ,
то
,
то
 ,
(4.2)
,
(4.2)
где
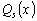 тоже
многочлен степени s. Кроме того, если
тоже
многочлен степени s. Кроме того, если
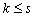 ,
то
,
то
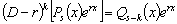 (4.3)
(4.3)
где
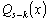 –
многочлен степени
–
многочлен степени 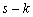 .
Если
.
Если 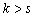 ,
то
,
то
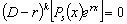 .
(4.4)
.
(4.4)
Доказательство. Сначала найдем выражение для
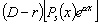 .
Имеем:
.
Имеем:

Так как 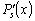 –
многочлен степени
–
многочлен степени 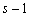 ,
то при
,
то при 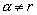 выражение
выражение
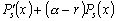 является
многочленом степени s. Но тогда и
является
многочленом степени s. Но тогда и
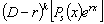 имеет
вид
имеет
вид 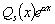 ,
где Qs(х) – многочлен степени s.
,
где Qs(х) – многочлен степени s.
Если 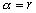 ,
то
,
то
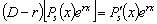 .
.
Поскольку 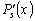 –
многочлен степени
–
многочлен степени 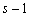 ,
то каждое применение оператора
,
то каждое применение оператора  понижает
на единицу степень множителя при
понижает
на единицу степень множителя при 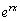 ,
а k-кратное применение этого оператора понижает
указанную степень на k. Отсюда и следует равенство (4.3) при
,
а k-кратное применение этого оператора понижает
указанную степень на k. Отсюда и следует равенство (4.3) при
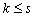 .
.
При k = s получаем, что
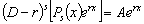 ,
где А — постоянная. Еще одно применение оператора
,
где А — постоянная. Еще одно применение оператора
 обращает
это выражение в нуль, поэтому при k > s
обращает
это выражение в нуль, поэтому при k > s
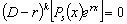 .
.
В частности, (D – r)×erx
= 0.
4.2. Общее решение однородного линейного дифференциального уравнения с
постоянными коэффициентами
Таким образом, решение однородных линейных дифференциальных
уравнений высшего порядка можно свести к решению алгебраических уравнений. В
частности, для решения таких уравнений второго порядка достаточно уметь решать
квадратные уравнения.
Теорема 4.3. Пусть характеристический
многочлен
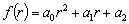 (4.5)
(4.5)
линейного дифференциального
уравнения второго порядка с постоянными коэффициентами
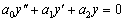 (4.6)
(4.6)
имеет два различных действительных
корня: 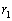 и
и
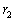 .
Тогда общее решение уравнения (2) имеет вид:
.
Тогда общее решение уравнения (2) имеет вид:
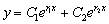 .
.
Доказательство. Уравнение (4.6) можно
записать в виде
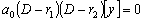 ,
,
причем множители
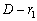 и
и
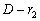 в
этом уравнении можно перестанавливать. Так как
в
этом уравнении можно перестанавливать. Так как
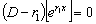 ,
то функция
,
то функция 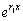 является
решением уравнения (4.6). Аналогично доказывается, что
является
решением уравнения (4.6). Аналогично доказывается, что
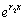 также
является его решением. Но тогда по следствию 3.1 любая линейная комбинация
также
является его решением. Но тогда по следствию 3.1 любая линейная комбинация
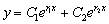 этих
решений также является решением заданного уравнения.
этих
решений также является решением заданного уравнения.
Чтобы доказать, что это решение является общим, надо
показать линейную независимость функций
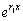 и
и
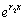 .
Вычислим определитель Вронского:
.
Вычислим определитель Вронского:

Поскольку 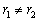 ,
а функция
,
а функция 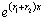 не
обращается в нуль ни при одном значении х, то
не
обращается в нуль ни при одном значении х, то
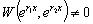 ,
и потому решения
,
и потому решения 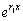 и
и
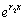 линейно
независимы.
линейно
независимы.
Аналогично доказывается, что если характеристический
многочлен уравнения 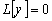 n-го
порядка имеет n различных корней
n-го
порядка имеет n различных корней
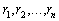 ,
то общее решение этого уравнения имеет вид:
,
то общее решение этого уравнения имеет вид:
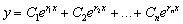 .
.
Пример 4.1. Найти общее решение уравнения
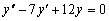 .
.
Решение. Составим характеристическое
уравнение
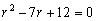 .
.
По теореме Виета имеем:
сумма корней характеристического уравнения
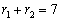 ;
;
произведение
корней
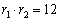 .
.
Этими свойствами обладают числа
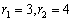 .
.
Значит, общее решение данного уравнения имеет вид:
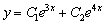 .
.
Рассмотрим теперь случай, когда корни
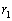 и
и
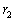 характеристического
уравнения
характеристического
уравнения  комплексны.
Так как мы рассматриваем лишь уравнения с действительными коэффициентами, то эти
корни комплексно сопряжены, т.е. имеют вид:
комплексны.
Так как мы рассматриваем лишь уравнения с действительными коэффициентами, то эти
корни комплексно сопряжены, т.е. имеют вид:
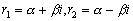 .
Но тогда общее решение дифференциального уравнения имеет вид:
.
Но тогда общее решение дифференциального уравнения имеет вид:
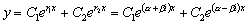 .
.
Преобразуем этот ответ к виду, не содержащему комплексных
чисел. По формуле Эйлера имеем:
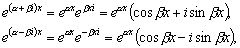
и потому
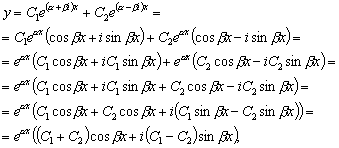
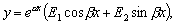 (4.7)
(4.7)
где
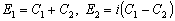 .
.
Чтобы доказать, что (4.7) является общим решением
дифференциального уравнения, осталось показать, что функции
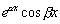 и
и
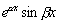 линейно
независимы.
линейно
независимы.
Это следует из того, что частное этих функций равно
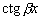 и
не является постоянным. Мы доказали следующую теорему:
и
не является постоянным. Мы доказали следующую теорему:
Теорема 4.4. Если корни
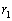 и
и
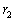 характеристического
уравнения для уравнения
характеристического
уравнения для уравнения
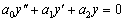
комплексно сопряжены:
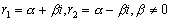 ,
то общее решение уравнения (4.8) имеет вид:
,
то общее решение уравнения (4.8) имеет вид:
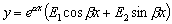 .
.
Пример 4.2. Решим уравнение
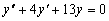 .
.
Решение. Характеристическое уравнение имеет
вид:
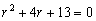 .
.
Дискриминант полученного квадратного уравнения
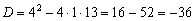 .
.
Корни уравнения комплексные сопряжённые:
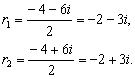
В данном случае
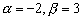 .
Значит, общее решение данного уравнения имеет вид:
.
Значит, общее решение данного уравнения имеет вид:
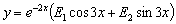 .
.
Аналогично записывается общее решение линейного однородного
дифференциального уравнения 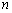 -го
порядка в случае, когда его характеристическое уравнение имеет комплексные
корни.
-го
порядка в случае, когда его характеристическое уравнение имеет комплексные
корни.
Нам осталось рассмотреть случай, когда характеристическое
уравнение  имеет
кратный корень
имеет
кратный корень 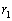 .
В этом случае оно имеет вид:
.
В этом случае оно имеет вид: 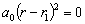 ,
a потому дифференциальное уравнение можно представить в виде
,
a потому дифференциальное уравнение можно представить в виде
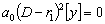 .
.
По следствию из теоремы 3.1 любая функция вида
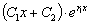 является
решением уравнения:
является
решением уравнения:
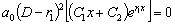 .
.
Эта функция является линейной комбинацией решений
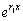 и
и
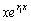 .
.
Покажем, что эти решения линейно независимы. В самом деле,
имеем:
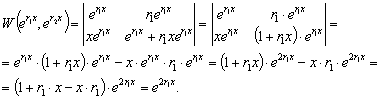
Поскольку 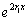 отлично
от нуля при любом х, то решения
отлично
от нуля при любом х, то решения
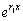 и
и
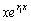 линейно
независимы, а потому
линейно
независимы, а потому 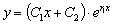 –
общее решение заданного дифференциального уравнения.
–
общее решение заданного дифференциального уравнения.
Мы доказали следующую теорему:
Теорема 4.5. Если характеристическое
уравнение для дифференциального уравнения
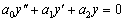
имеет корень
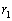 второй
кратности, то общее решение для этого уравнения имеет вид:
второй
кратности, то общее решение для этого уравнения имеет вид:
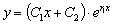
Пример 4.3. Найдем общее решение уравнения
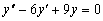 .
.
Решение. Составим характеристическое
уравнение
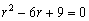 .
.
Оно имеет корень
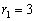 второй
кратности. Значит, его общее решение имеет вид:
второй
кратности. Значит, его общее решение имеет вид:
 .
.
Если L[у] = 0 – однородное линейное
дифференциальное уравнение n-го порядка и
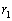 –
корень соответствующего характеристического уравнения, имеющий кратность k,
то ему соответствует в общем решении группа слагаемых вида
–
корень соответствующего характеристического уравнения, имеющий кратность k,
то ему соответствует в общем решении группа слагаемых вида
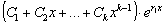 ,
,
т.е. линейная комбинация решений
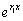 ,
,
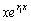 ,...,
,...,
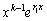 .
.
Линейная независимость решений
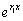 ,
,
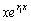 ,...,
,...,
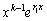
может быть доказана без ссылки на
определитель Вронского. Пусть равенство
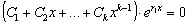 (4.8)
(4.8)
выполняется для всех значений х.
Так как 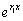 не
обращается в нуль ни при одном значении х, то многочлен
не
обращается в нуль ни при одном значении х, то многочлен
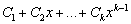
тождественно равен нулю. А это
может быть лишь при условии, что все коэффициенты
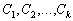 этого
многочлена равны нулю.
этого
многочлена равны нулю.
Итак, равенство (4.8) выполняется лишь при условии, что
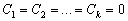 .
А это и значит, что решения
.
А это и значит, что решения 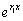 ,
,
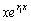 ,...,
,...,
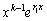 линейно
независимы.
линейно
независимы.
4.3. Решение неоднородного линейного дифференциального уравнения с
постоянными коэффициентами (специальные случаи)
Мы умеем решать любое однородное линейное дифференциальное
уравнение с постоянными коэффициентами L[у] = 0. Применяя метод
вариации произвольных постоянных, можно найти и частное решение любого уравнения
вида 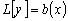 .
Однако в наиболее важных для практики случаях, когда правая часть уравнения
имеет вид:
.
Однако в наиболее важных для практики случаях, когда правая часть уравнения
имеет вид:
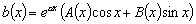 (4.9)
(4.9)
(где А(х) и В(х)
– многочлены), можно найти частное решение уравнения
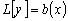 ,
не прибегая к методу вариации произвольных постоянных.
,
не прибегая к методу вариации произвольных постоянных.
Предложим без доказательства таблицу, определяющую сводку
правил отыскания частного решения линейного неоднородного уравнения второго
порядка с постоянными коэффициентами в зависимости от вида правой части
уравнения:
|
№ п/п |
Вид правой части |
Корни характеристического
уравнения |
Вид частного решения уравнения |
|
1 |
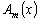 –
многочлен степени –
многочлен степени
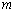 . . |
Число 0 не является корнем
характеристического уравнения |
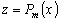 |
|
|
Число 0 является корнем
характеристического уравнения кратности s |
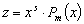 |
|
2 |
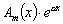 |
Число
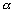 не
является корнем характеристического уравнения не
является корнем характеристического уравнения |
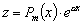 |
|
|
Число
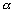 является
корнем характеристического уравнения кратности s является
корнем характеристического уравнения кратности s |
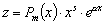 |
|
3 |
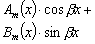 |
Числа ±bi
не являются корнями характеристического уравнения |
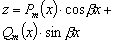 |
|
|
Числа ±bi
являются корнями характеристического уравнения кратности
s |
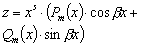 |
|
4 |
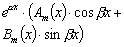 |
Числа α±bi
не являются корнями характеристического уравнения |
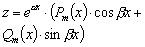 |
|
|
Числа α±bi
являются корнями характеристического уравнения кратности
s |
 |
Пример 4.4.
Найти решение уравнения
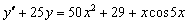 ,
,
удовлетворяющее начальным условиям:
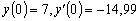 .
.
Решение.
Соответствующее однородное уравнение имеет вид:
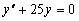 .
.
Характеристическое уравнение:
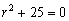 .
.
Корни характеристического уравнения:
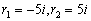 .
.
Общее решение однородного уравнения:
 .
.
Правую часть уравнения можно рассматривать как сумму
функций
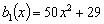 ,
,
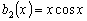 .
.
Рассмотрим два вспомогательных уравнения:
 (4.10)
(4.10)
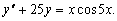 (4.11)
(4.11)
Поскольку в уравнении (4.10) число 0 не является корнем
характеристического уравнения, то его частное решение будем искать в виде
многочлена второй степени:
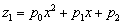 .
.
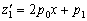 ,
,
 .
.
Подставляем полученное в уравнение (4.10):

Переходим к системе:
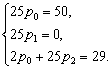
Отсюда
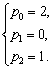
И
 .
.
В уравнении (4.11)
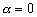 ,
,
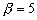 ,
,
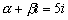 ,
,
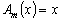 –
многочлен первой степени.
–
многочлен первой степени.
Как видим, число
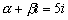 является
корнем характеристического уравнения. С учётом этого частное решение надо искать
по формуле:
является
корнем характеристического уравнения. С учётом этого частное решение надо искать
по формуле:
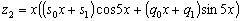 .
.
Дифференцируем:
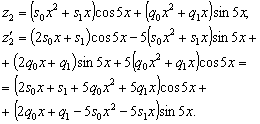
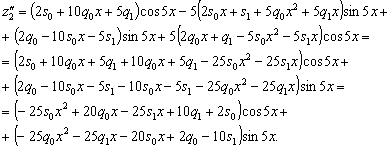
Подставляем полученное в уравнение (4.11):
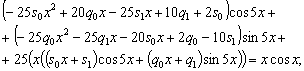
Упрощаем:
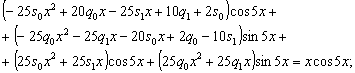
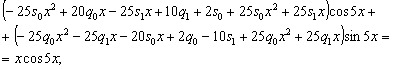
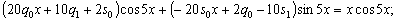
Переходим к системе:

Решение системы:
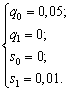
Тогда частное решение уравнения (4.11):
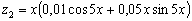 .
.
Поэтому функция
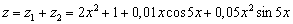
является частным решением данного
уравнения.
Поэтому общим решением данного уравнения является функция:
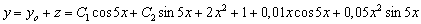 .
.
Применим начальные условия. Для этого найдём производную:
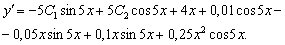
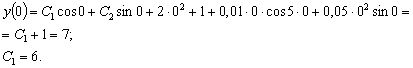

И решение задачи Коши запишется в виде:
 .
.
К содержанию
Составитель к.ф.-м.н. Подклетнова С.В.
![]() ,
,![]() .
.![]() .
.![]() .
.![]() .
.![]() .
.![]() ,
,![]() .
.![]() (4.10)
(4.10)![]() (4.11)
(4.11)![]() .
.![]() ,
,![]() .
.![]()
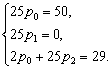
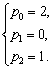
![]() .
.![]() ,
,
![]() ,
,
![]() ,
,
![]() –
многочлен первой степени.
–
многочлен первой степени.![]() является
корнем характеристического уравнения. С учётом этого частное решение надо искать
по формуле:
является
корнем характеристического уравнения. С учётом этого частное решение надо искать
по формуле:![]() .
.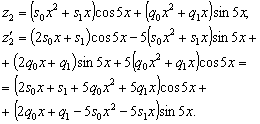
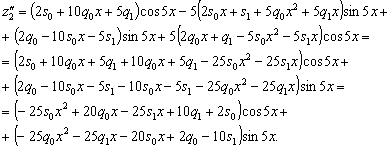
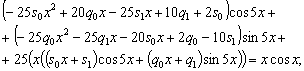
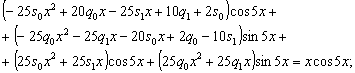
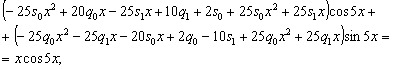
![]()

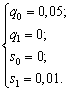
![]() .
.![]()
![]() .
.![]()
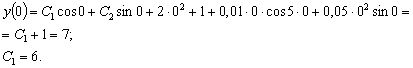

![]() .
.