К содержанию
Составитель к.ф.-м.н. Подклетнова С.В.
Дополнительные материалы.
Численные методы Эйлера и Рунге-Кутта
1. Постановка исходной задачи
Будем рассматривать
задачу Коши для системы обыкновенных дифференциальных уравнений
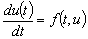 ,
,
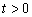 ,
,
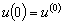 .
(д.1)
.
(д.1)
или, подробнее,
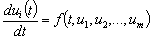 ,
,
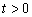 ,
,
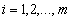 ,
(д.2)
,
(д.2)
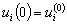 ,
,
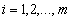 .
(д.3)
.
(д.3)
Предположим, что
функции 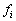 ,
,
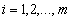 непрерывны
по всем аргументам в замкнутой области
непрерывны
по всем аргументам в замкнутой области
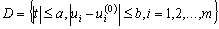 .
.
Из непрерывности
функций 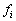 следует
их ограниченность, т.е. существование константы
следует
их ограниченность, т.е. существование константы
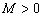 такой,
что всюду в D выполняются неравенства
такой,
что всюду в D выполняются неравенства
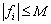 ,
,
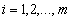 .
.
Предположим, кроме
того, что в D функции 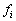 удовлетворяют
условию Липшица по аргументам
удовлетворяют
условию Липшица по аргументам 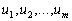 ,
т.е.
,
т.е.

для любых точек
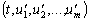 и
и
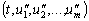 области
D.
области
D.
Если выполнены
сформулированные выше предположения, то существует единственное решение
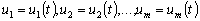
системы (д.2), определенное при
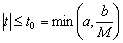 и
принимающее при
и
принимающее при 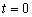 заданные
начальные значения (д.3).
заданные
начальные значения (д.3).
При исследовании
численных методов для задачи Коши будем заранее предполагать, что её решение
существует, единственно и обладает необходимыми свойствами гладкости.
2. Примеры численных методов
Существуют две группы
численных методов решения задачи Коши: многошаговые разностные методы и методы
Рунге-Кутта. Приведем примеры и поясним основные понятия, возникающие при
использовании численных методов. Для простоты изложения будем рассматривать
сейчас одно уравнение
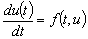 ,
,
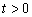 ,
,
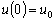 .
(д.4)
.
(д.4)
Введем по переменному
t равномерную сетку с шагом  ,
т.е. рассмотрим множество точек
,
т.е. рассмотрим множество точек
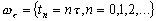
Будем обозначать
через u(t) точное решение задачи (д.4), а через
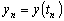 —
приближенное решение. Заметим, что приближенное решение является сеточной
функцией, т.е. определено только в точках сетки сот.
—
приближенное решение. Заметим, что приближенное решение является сеточной
функцией, т.е. определено только в точках сетки сот.
Пример 1.
Метод Эйлера. Уравнение (д.4) заменяется разностным уравнением
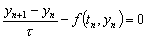 ,
,
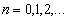 ,
,
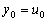 .
(д.5)
.
(д.5)
Решение этого
уравнения находится явным образом по рекуррентной формуле
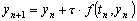 ,
,
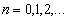 ,
,
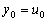 .
.
При использовании
приближенных методов основным является вопрос о сходимости. Понятие сходимости
приближенного метода можно сформулировать по-разному. Применительно к разностным
методам, к которым относится и метод Эйлера д.5), наибольшее распространение
получило понятие сходимости при 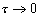 .
Оно означает следующее. Фиксируем точку t и построим последовательность
сеток
.
Оно означает следующее. Фиксируем точку t и построим последовательность
сеток 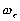 таких,
что
таких,
что 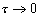 и
и
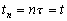 (тогда
необходимо
(тогда
необходимо 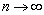 ).
Говорят, что метод (д.5) сходится в точке t, если
).
Говорят, что метод (д.5) сходится в точке t, если
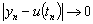 при
при
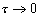 ,
tn = t.
,
tn = t.
Метод сходится на
отрезке 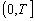 ,
если он сходится в каждой точке
,
если он сходится в каждой точке 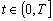 .
.
Говорят, что метод
имеет р-й порядок точности, если существует число р > 0 такое, что
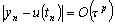 при
при
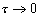 .
.
Получим уравнение,
которому удовлетворяет погрешность метода
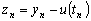 .
Подставляя
.
Подставляя 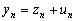 в
(д.5), получим
в
(д.5), получим
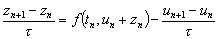 (д.6)
(д.6)
Правую часть
уравнения (д.6) можно представить в виде суммы
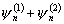 ,
,
где
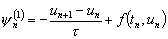 ,
,
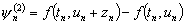 .
.
Функция
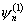 называется
невязкой или погрешностью аппроксимации разностного уравнения (д.5) на решении
исходного уравнения (д.4). Видно, что невязка представляет собой результат
подстановки точного решения
называется
невязкой или погрешностью аппроксимации разностного уравнения (д.5) на решении
исходного уравнения (д.4). Видно, что невязка представляет собой результат
подстановки точного решения 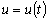 в
левую часть разностного уравнения (д.5). Если бы приближенное решение
в
левую часть разностного уравнения (д.5). Если бы приближенное решение
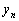 совпадало
с точным
совпадало
с точным 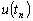 ,
то невязка равнялась бы нулю. Говорят, что разностный метод аппроксимирует
исходное дифференциальное уравнение, если
,
то невязка равнялась бы нулю. Говорят, что разностный метод аппроксимирует
исходное дифференциальное уравнение, если
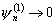 при
при
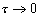 .
Разностный метод имеет р-й порядок аппроксимации, если
.
Разностный метод имеет р-й порядок аппроксимации, если
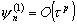 .
В дальнейшем будет показано, что при очень общих предположениях порядок точности
разностного метода совпадает с порядком аппроксимации. Функция
.
В дальнейшем будет показано, что при очень общих предположениях порядок точности
разностного метода совпадает с порядком аппроксимации. Функция
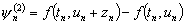
обращается в нуль, если правая часть
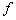 не
зависит от решения
не
зависит от решения 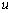 .
В общем случае
.
В общем случае 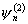 пропорциональна
погрешности
пропорциональна
погрешности 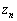 ,
так как по формуле конечных приращений имеем
,
так как по формуле конечных приращений имеем
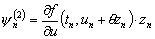 ,
,
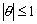 .
.
Порядок аппроксимации
метода Эйлера (д.5) нетрудно найти, используя разложение по формуле Тейлора.
Поскольку
 ,
,
то в силу уравнения (д.4)
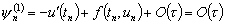 ,
,
т.е. метод Эйлера имеет первый порядок аппроксимации. При
выводе предполагалась ограниченность
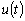 .
.
Пример 2.
Метод Рунге-Кутта второго порядка точности. Предположим, что приближенное
значение 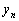 решения
исходной задачи в момент t = tn уже известно. Для
нахождения
решения
исходной задачи в момент t = tn уже известно. Для
нахождения 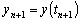 поступим
следующим образом. Сначала, используя схему Эйлера
поступим
следующим образом. Сначала, используя схему Эйлера
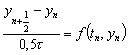 ,
(д.7)
,
(д.7)
вычислим промежуточное значение
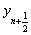 ,
а затем воспользуемся разностным уравнением
,
а затем воспользуемся разностным уравнением
 ,
(д.8)
,
(д.8)
из которого явным образом найдем искомое значение
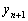 .
.
Для исследования
невязки подставим промежуточное значение
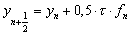 ,
где
,
где 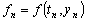 ,
в уравнение (д.8). Тогда получим разностное уравнение
,
в уравнение (д.8). Тогда получим разностное уравнение
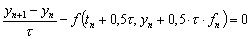 (д.9)
(д.9)
невязка которого равна
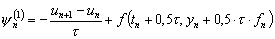 (д.10)
(д.10)
Имеем
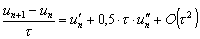 ,
,
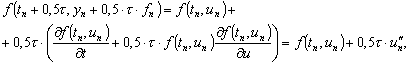
так как в силу (д.4) справедливо равенство
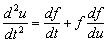 .
.
Таким образом, метод
(д.9) имеет второй порядок погрешности аппроксимации,
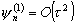 и
является явным.
и
является явным.
Реализация метода
(д.9) в виде двух этапов (д.7), (д.8) называется методом предиктор-корректор (предсказывающе-исправляющим),
поскольку на первом этапе (д.7) приближенное значение предсказывается с
невысокой точностью 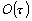 ,
а на втором этапе (д.8) это предсказанное значение исправляется, так что
результирующая погрешность имеет второй порядок по
,
а на втором этапе (д.8) это предсказанное значение исправляется, так что
результирующая погрешность имеет второй порядок по
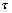 .
.
Тот же самый метод
(д.9) можно реализовать несколько иначе. А именно, сначала вычислим
последовательно функции
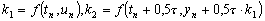 ,
,
а затем найдем
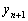 из
уравнения
из
уравнения
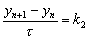 .
.
Такая форма
реализации метода (д.9) называется методом Рунге- Кутта. Поскольку требуется
вычислить две промежуточные функции,
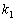 и
k2, данный метод относится к двухэтапным методам. Существуют и
более общие m-этапные методы Рунге-Кутта,
позволяющие получить большую точность.
и
k2, данный метод относится к двухэтапным методам. Существуют и
более общие m-этапные методы Рунге-Кутта,
позволяющие получить большую точность.
К содержанию