 Занятие
№ 3. Поток векторного поля
Занятие
№ 3. Поток векторного поля
Задание 3.1. Дать определение потока
векторного поля.
Задание 3.2. Дать определение поверхностного
интеграла.
Задание 3.3. Показать физический смысл потока
векторного поля.
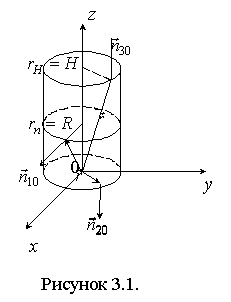
Пример 3.1. Найти поток поля радиус-вектора
точки 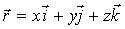 через
прямой цилиндр радиуса
через
прямой цилиндр радиуса 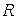 с
центром в начале координат и высоты
с
центром в начале координат и высоты 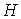 (рис.
3.1).
(рис.
3.1).
Решение. Для вычисления потока вектора
используем формулу
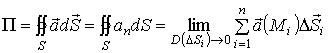 .
.
Согласно условию задачи поверхность
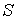 состоит
из боковой поверхности и двух оснований цилиндра. Поток записывается в виде
суммы поверхностных интегралов:
состоит
из боковой поверхности и двух оснований цилиндра. Поток записывается в виде
суммы поверхностных интегралов:
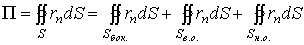 .
.
На боковой поверхности внешняя нормаль
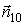 параллельна
плоскости
параллельна
плоскости 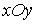 и
проекция на нее
и
проекция на нее 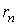 равна
равна
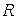 ,
а площадь боковой поверхности цилиндра
,
а площадь боковой поверхности цилиндра
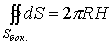 .
Следовательно,
.
Следовательно,
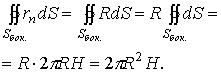
На нижнем основании радиус-вектор
 перпендикулярен
нормали
перпендикулярен
нормали 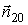 и
и
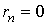 .
Поэтому
.
Поэтому 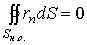 .
На верхнем основании нормаль
.
На верхнем основании нормаль  направлена
относительно оси
направлена
относительно оси 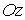 вверх
и
вверх
и 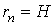 ,
а площадь основания цилиндра
,
а площадь основания цилиндра 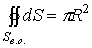 .
Следовательно,
.
Следовательно,
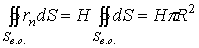 .
.
Тогда поток поля радиус-вектора точки
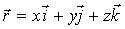 через
прямой цилиндр радиуса
через
прямой цилиндр радиуса 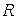 с
центром в начале координат и высоты
с
центром в начале координат и высоты 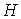 равен:
равен:
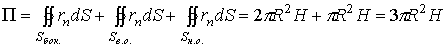 .
.
Ответ.
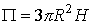 .
.
Пример
3.2. Найти поток поля вектора
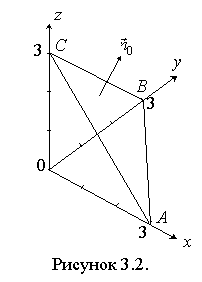
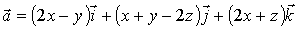
через часть плоскости
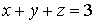 ,
лежащую в первом квадранте.
,
лежащую в первом квадранте.
Решение. Найдем линию пересечения данной
плоскости с координатной плоскостью 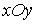 .
Для этого положим
.
Для этого положим 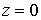 .
Тогда
.
Тогда
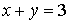 .
.
Линия пересечения данной плоскости с координатной
плоскостью 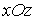 (
(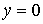 )
задается уравнением
)
задается уравнением
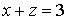 ,
,
а линия пересечения данной
плоскости с координатной плоскостью 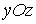 (
(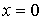 )
– уравнением
)
– уравнением
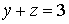 .
.
Вычислим поток поля через площадь треугольника
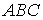 (рисунок
3.2).
(рисунок
3.2).
За положительное направление нормали
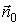 к
плоскости треугольника примем направление от начала координат:
к
плоскости треугольника примем направление от начала координат:
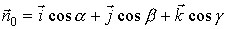 .
.
Тогда
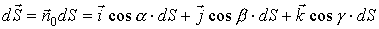 .
.
Так как в нашем случае все направляюще косинусы
положительны, имеем
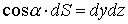 ;
;
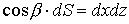 ;
;
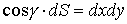 .
.
Поэтому
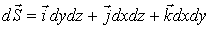 ,
,
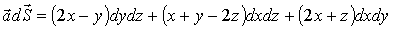 .
.
Искомый поток поля будет состоять из трех поверхностных
интегралов по площади треугольника 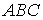 :
:
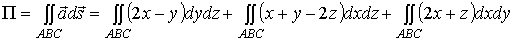 .
.
Каждый из этих трех поверхностных интегралов заменим
двойным интегралом, являющимся проекцией треугольника на соответствующую
координатную плоскость.
Поверхностный интеграл
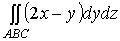 отличается
от двойного
отличается
от двойного 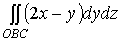 лишь
тем, что в интеграле по
лишь
тем, что в интеграле по 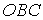 координата
координата
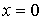 ,
а в интеграле по
,
а в интеграле по 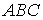
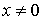 ;
в нем
;
в нем 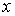 зависит
от
зависит
от 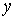 и
и
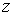 .
Эта зависимость определяется уравнением плоскости треугольника:
.
Эта зависимость определяется уравнением плоскости треугольника:
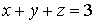 ,
так что на плоскости треугольника
,
так что на плоскости треугольника 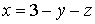 .
Поэтому
.
Поэтому
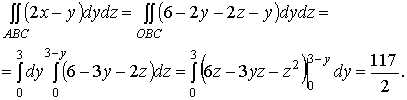
Аналогично заменяются и два других поверхностных интеграла
двойными:
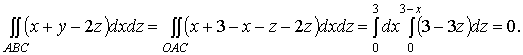
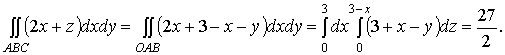
Отсюда
 .
.
Ответ.
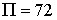 .
.
Упражнения.
1.
Найти поток поля радиуса-вектора точки
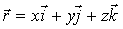 через
поверхность прямого конуса, вершина которого в начале координат, радиуса
через
поверхность прямого конуса, вершина которого в начале координат, радиуса
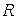 и
высоты
и
высоты 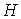 .
.
2.
Найти поток вектора 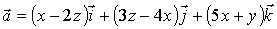 через
часть плоскости
через
часть плоскости 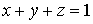 ,
лежащую в первом квадранте.
,
лежащую в первом квадранте.
3.
Найти поток векторного поля 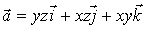 через
поверхность пирамиды с вершиной в точке
через
поверхность пирамиды с вершиной в точке
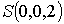 и
основанием
и
основанием 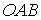 ,
где
,
где 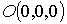 ,
,
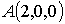 ,
,
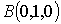 .
.
4.
Найти поток векторного поля 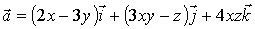 через
поверхность пирамиды, ограниченную плоскостями
через
поверхность пирамиды, ограниченную плоскостями
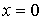 ,
,
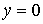 ,
,
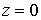 ,
,
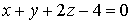 .
.
5.
Вычислить поток векторного поля
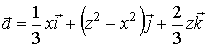 через
полную поверхность цилиндра:
через
полную поверхность цилиндра: 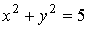 ;
;
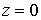 ;
;
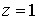 .
.